A Brief Introduction to Linear Attentions

This is a blog version of my slides on the topic of linear attentions. The slides were presented during the weekly group meeting/study group in our team. The storyline is highly inspired by ¹.

Motivation

Attention and recurrent modules can be seen as token-mixing modules. They blend signals across the sequence domain, in contrast to FFNs or MLPs, which operate within the scope of a single token.

However, softmax attention and recurrent modules come with their own strengths and weaknesses.

	Recurrent	Softmax Attention	Linear Attention
Training	Sequential	Parallelizable	Parallelizable?
Inference	Linear	Quadratic	Linear?
Performance	OK?	Strong	?

Linear attention tries to combine the best of both worlds.

²

Softmax Attention

$$\begin{array}{c}{\mathbf{q}}_i,{\mathbf{k}}_i,{\mathbf{v}}_i,{\mathbf{o}}_i\in {\mathbb{R}}^{d\times 1}\\ \mathbf{Q}={\left[\begin{array}{cccc}{\mathbf{q}}_1& {\mathbf{q}}_2& \dots & {\mathbf{q}}_n\end{array}\right]}^{\top }\in {\mathbb{R}}^{n\times d}\\ \mathbf{K}={\left[\begin{array}{cccc}{\mathbf{k}}_1& {\mathbf{k}}_2& \dots & {\mathbf{k}}_n\end{array}\right]}^{\top }\in {\mathbb{R}}^{n\times d}\\ \mathbf{V}={\left[\begin{array}{cccc}{\mathbf{v}}_1& {\mathbf{v}}_2& \dots & {\mathbf{v}}_n\end{array}\right]}^{\top }\in {\mathbb{R}}^{n\times d}\\ \mathbf{O}={\left[\begin{array}{cccc}{\mathbf{o}}_1& {\mathbf{o}}_2& \dots & {\mathbf{o}}_n\end{array}\right]}^{\top }\in {\mathbb{R}}^{n\times d}\end{array}$$ $${\mathbf{o}}_t=\frac{{\sum }_{i=1}^t\exp \left({\mathbf{q}}_t^{\top }{\mathbf{k}}_i\right){\mathbf{v}}_i}{{\sum }_{j=1}^t\exp \left({\mathbf{q}}_t^{\top }{\mathbf{k}}_j\right)},\mathbf{O}=\text{softmax}\left(\left(\mathbf{Q}{\mathbf{K}}^{\top }\right)\odot \mathbf{M}\right)\mathbf{V},\mathbf{M}\text{ is causal mask}$$

• Inference:
  • Each step is ${\sum }_{i=1}^t\exp \left({\mathbf{q}}_t^{\top }{\mathbf{k}}_i\right){\mathbf{v}}_i⟹O(nd)$
  • Overall complexity is $O(n^2)$ when $d\ll n$.
• Training: can be parallelized with matrix form. Causality is realized by the causal mask.

Linear Attention: Variants and Perspectives

Vanilla Linear Attention

$${\mathbf{o}}_t=\frac{{\sum }_{i=1}^t\exp \left({\mathbf{q}}_t^{\top }{\mathbf{k}}_i\right){\mathbf{v}}_i}{{\sum }_{j=1}^t\exp \left({\mathbf{q}}_t^{\top }{\mathbf{k}}_j\right)}=\frac{{\sum }_{i=1}^t{\mathbf{v}}_i\cdot \exp \left({\mathbf{k}}_i^{\top }{\mathbf{q}}_t\right)}{{\sum }_{j=1}^t\exp \left({\mathbf{k}}_j^{\top }{\mathbf{q}}_t\right)}$$

• Bottleneck is ${\sum }_{i=1}^t{\mathbf{v}}_i\cdot \exp \left({\mathbf{k}}_i^{\top }{\mathbf{q}}_t\right)$ $⟹$ can we remove $\exp$?
• Replace $\exp \left({\mathbf{k}}_i^{\top }{\mathbf{q}}_t\right)$ with kernel trick $\varphi ({\mathbf{k}}_i{)}^T\varphi ({\mathbf{q}}_t)$³, where $\varphi (\cdot ):{\mathbb{R}}^n\to {\mathbb{R}}^m$.

$${\mathbf{o}}_t=\frac{{\sum }_{i=1}^t{\mathbf{v}}_i\cdot \left(\varphi ({\mathbf{k}}_i{)}^{\top }\varphi ({\mathbf{q}}_t)\right)}{{\sum }_{j=1}^t\varphi ({\mathbf{k}}_j{)}^T\varphi ({\mathbf{q}}_t)}=\frac{\left({\sum }_{i=1}^t{\mathbf{v}}_i\cdot \varphi ({\mathbf{k}}_i{)}^{\top }\right)\varphi ({\mathbf{q}}_t)}{\left({\sum }_{j=1}^t\varphi ({\mathbf{k}}_i{)}^{\top }\right)\varphi ({\mathbf{q}}_t)}=\frac{{\mathbf{S}}_t\varphi ({\mathbf{q}}_t)}{{\mathbf{z}}_t^{\top }\varphi ({\mathbf{q}}_t)}$$

• Recent works⁴⁵ discovered that a linear kernel ($\varphi =\mathbf{I}$) and no normalizer works well in practice. $${\mathbf{o}}_t={\mathbf{S}}_t{\mathbf{q}}_t,{\mathbf{S}}_t={\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top },{\mathbf{S}}_t\in {\mathbb{R}}^{d\times d}$$ $$\mathbf{O}=\left(\mathbf{Q}{\mathbf{K}}^{\top }\odot \mathbf{M}\right)\mathbf{V}$$
• During inference:
  • State ${\mathbf{S}}_t$ is now $O(d^2)\to O(1)$ space.
  • Each token update is $O(d^2)\to O(1)$ time.
• We have solved the quadratic complexity issue!
• What about training?
  • Ideally we’d like $\mathbf{O}=(\mathbf{Q}{\mathbf{K}}^{\top })\mathbf{V}=\mathbf{Q}({\mathbf{K}}^{\top }\mathbf{V})⟹O(n^{2}d)\to O(n{d}^2)⟹$ ❌ due to $\odot \mathbf{M}$.

Chunkwise Parallel Form

The chunkwise parallel form aims to balance between parallel and recurrent form. Subquadratic, partially parallel training.

1. Input is split into non-overlapping chunks with length $c$. Number of chunks is $\frac{n}{c}$.

2. For each chunk $i\in [0,1,\dots ,\frac{n}{c}-1]$, calculate

   $${\mathbf{S}}_{[i+1]}={\mathbf{S}}_{[i]}+\sum _{j=ic+1}^{(i+1)c}{\mathbf{k}}_j^{\top }{\mathbf{v}}_j={\mathbf{S}}_{[i]}+{\mathbf{K}}_{[i]}^{\top }{\mathbf{V}}_{[i]}$$

   ${\mathbf{K}}_{[i]}^{\top }{\mathbf{V}}_{[i]}$ can be calculated in $O(c^{2}d)$ in parallel $⟹O(\frac{n}{c}{c}^{2}d)=O(ncd)$

3. Similarly, calculate output

   $${\mathbf{O}}_{[i+1]}=\underset{\text{inter-chunk: }O(c{d}^2)}{\underbrace{{\mathbf{Q}}_{[i+1]}{\mathbf{S}}_{[i]}}}+\underset{\text{intra-chunk: }O(c^{2}d+c{d}^2)}{\underbrace{\left(\left({\mathbf{Q}}_{[i+1]}{\mathbf{K}}_{[i+1]}^{\top }\right)\odot \mathbf{M}\right){\mathbf{V}}_{[i+1]}}}$$

Training complexity is thus $O(\frac{n}{c}(c{d}^2+c^{2}d+c{d}^2))=O(ncd+2n{d}^2)<O(n^{2}d)$ when $d<n$.

Problems of Vanilla Linear Attention

²

• Performance
  • Linear attention is basically cumsum.
  • State/memory ${\mathbf{S}}_t$ size is constant.
  • When sequence length $n$ is long enough, the rank of ${\mathbf{S}}_t$ would be less than $n$, leading to key collisions.
• Training Efficiency
  • Chunkwise parallel form is required for approximate parallel training.

RetNet²

• Motivation:
  • Vanilla linear attention performs worse than softmax attention.
  • Forget gates has been shown to be crucial in RNNs, but training is sequential.
• Methodology:
  • Introduced a data-independent, scalar forgetting factor $\gamma ⟹{\mathbf{S}}_t=\gamma {\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top },{\mathbf{o}}_t={\mathbf{S}}_t{\mathbf{q}}_t$
  • Derived both recurrent and chunkwise parallel form.

The Mamba Series⁶⁷

• Started from State Space Model (SSM): $${\mathbf{h}}_t^{\prime }=\mathbf{A}{\mathbf{h}}_t+\mathbf{B}{\mathbf{x}}_t{\mathbf{y}}_t=\mathbf{C}{\mathbf{h}}_t$$
• Mamba: $${\mathbf{S}}_t=\exp \left(-\left({\mathbf{\alpha }}_t{1}^{\top }\right)\odot \exp \left(\mathbf{A}\right)\right)\odot {\mathbf{S}}_{t-1}+\left({\mathbf{\alpha }}_t\odot {\mathbf{v}}_t\right){\mathbf{k}}_t^{\top }{\mathbf{o}}_t={\mathbf{S}}_t{\mathbf{q}}_t+\mathbf{d}\odot {\mathbf{v}}_t$$
  • However, training cannot be parallelized.
• Mamba-2: simplified to improve training efficiency. $${\mathbf{S}}_t={\gamma }_t{\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }{\mathbf{o}}_t={\mathbf{S}}_t{\mathbf{q}}_t$$
  • Different from RetNet, ${\gamma }_t\in (0,1)$ is data-dependent.

GLA⁸

$${\mathbf{S}}_t={\mathbf{G}}_t\odot {\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top },{\mathbf{G}}_t\in (0,1{)}^{d_k\times d_k}$$

• Motivation: effectively and efficiently parametrize forgetting gate.
  • RetNet: data-independent scalar.
  • Mamba: data-dependent, but no parallelize training, and hardware inefficient.
  • Mamba2: parallelizable training. ${\mathbf{G}}_t={\gamma }_{t}11^{\top }$
• Methodology: $$\begin{array}{c}{\mathbf{G}}_t={\mathbf{\alpha }}_t{1}^{\top }\\ {\alpha }_t=\sigma \left({\mathbf{W}}_{{\alpha }^{+}}\cdot {\mathbf{W}}_{{\alpha }^{-}}\cdot {\mathbf{x}}_t\right)\\ {\mathbf{S}}_t=\left({\mathbf{\alpha }}_t{1}^{\top }\right)\odot {\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }=\text{Diag}({\mathbf{\alpha }}_{\mathbf{t}}){\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }\end{array}$$
  • Forgetting gate ${\mathbf{\alpha }}_t$ is now column-wise instead of global.

DeltaNet⁹

Motivation: forgetting factor design from a fast weight programming perspective.

• Original recurrent module: ${\mathbf{o}}_t={\mathbf{S}}_t{\mathbf{q}}_t,{\mathbf{S}}_t={\mathbf{S}}_{t-1}+{\mathbf{v}}_t{\mathbf{k}}_t^{\top }$
• Formulate it as a deep-learning problem:
  • Model: $f\left(\mathbf{S};\mathbf{x}\right)=\mathbf{S}\mathbf{x}$ where $\mathbf{S}$ is the model weights.
  • Training: $\mathbf{v}=f\left(\mathbf{S};\mathbf{k}\right)$
  • Inference: $\mathbf{o}=f\left(\mathbf{S};\mathbf{q}\right)$
  • Weight update rule: $\mathbf{S}={\mathbf{S}}_{t-1}+\mathbf{v}{\mathbf{k}}^{\top }⟹$ What does this mean?
    • Learning rate $\eta =1$
    • ${\nabla }_{\mathbf{S}}\mathcal{L}\left(f\left(\mathbf{S};\mathbf{k}\right),\mathbf{v}\right)=-\mathbf{v}{\mathbf{k}}^{\top }$
    • $\mathcal{L}=-{\mathbf{v}}^{\top }\left(\mathbf{S}\mathbf{k}\right)=-⟨f\left(\mathbf{S};\mathbf{k}\right),\mathbf{v}⟩⟹$ maximize inner-product

💡 Any better ways to do this?

• Model: $f\left(\mathbf{S};\mathbf{x}\right)=\mathbf{S}\mathbf{x}$
• Loss function: $\mathcal{L}=\frac{1}{2}{\Vert \mathbf{S}\mathbf{k}-\mathbf{v}\Vert }^2$
• Gradient:${\nabla }_{\mathbf{S}}\mathcal{L}=\left(\mathbf{S}\mathbf{k}-\mathbf{v}\right){\mathbf{k}}^{\top }$
• Update rule:${\mathbf{S}}_t={\mathbf{S}}_{t-1}-{\beta }_t\left({\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t\right){\mathbf{k}}_t^{\top }$

And there we have DeltaNet.

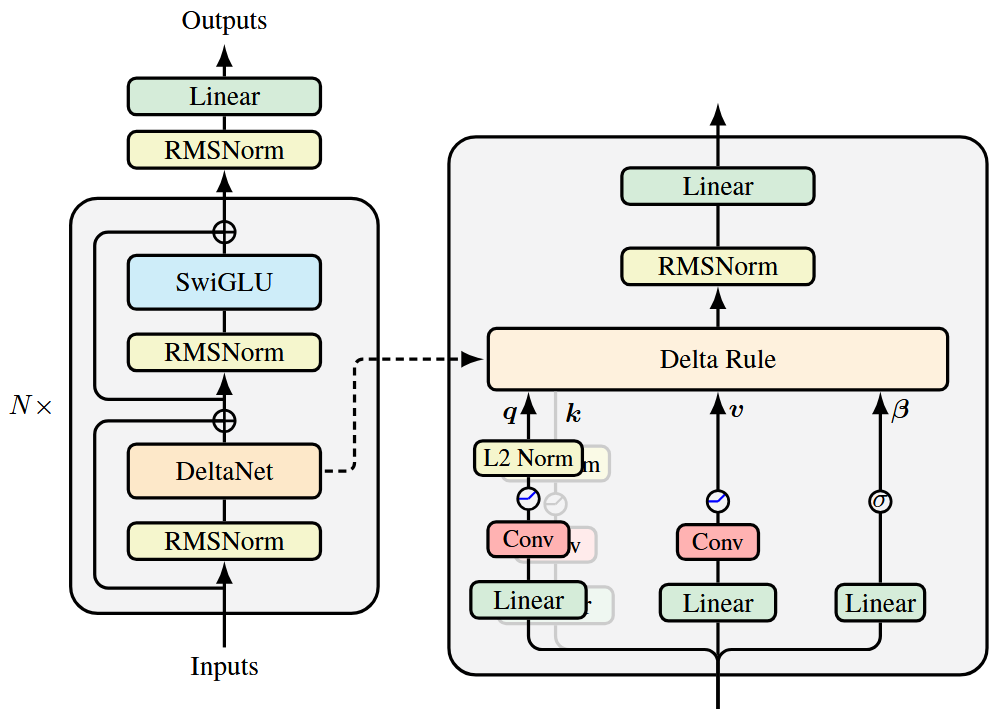
Note that the convolutions in the image are depthwise separable convolutions.

Alternative Interpretation: Key-Value Retrieval

The Delta Rule:

$${\mathbf{S}}_t={\mathbf{S}}_{t-1}-{\beta }_t\left({\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t\right){\mathbf{k}}_t^{\top }$$

1. Retrieves the old value using the current key ${\mathbf{v}}_t^{\text{old}}={\mathbf{S}}_{t-1}{\mathbf{k}}_t$.
2. Obtains a new value ${\mathbf{v}}_t^{\text{new}}$ by interpolating between the old value and the current new value ${\mathbf{v}}_t$, which replaces ${\mathbf{v}}_t^{\text{old}}$ in the memory.

$$\begin{array}{c}{\mathbf{v}}_t^{\text{new}}={\beta }_t{\mathbf{v}}_t+(1-{\beta }_t){\mathbf{v}}_t^{\text{old}}\\ \\ {\mathbf{S}}_t={\mathbf{S}}_{t-1}\underset{\text{remove}}{\underbrace{-{\mathbf{v}}_t^{\text{old}}{\mathbf{k}}_t^{\top }}}\underset{\text{write}}{\underbrace{+{\mathbf{v}}_t^{\text{new}}{\mathbf{k}}_t^{\top }}}\end{array}$$

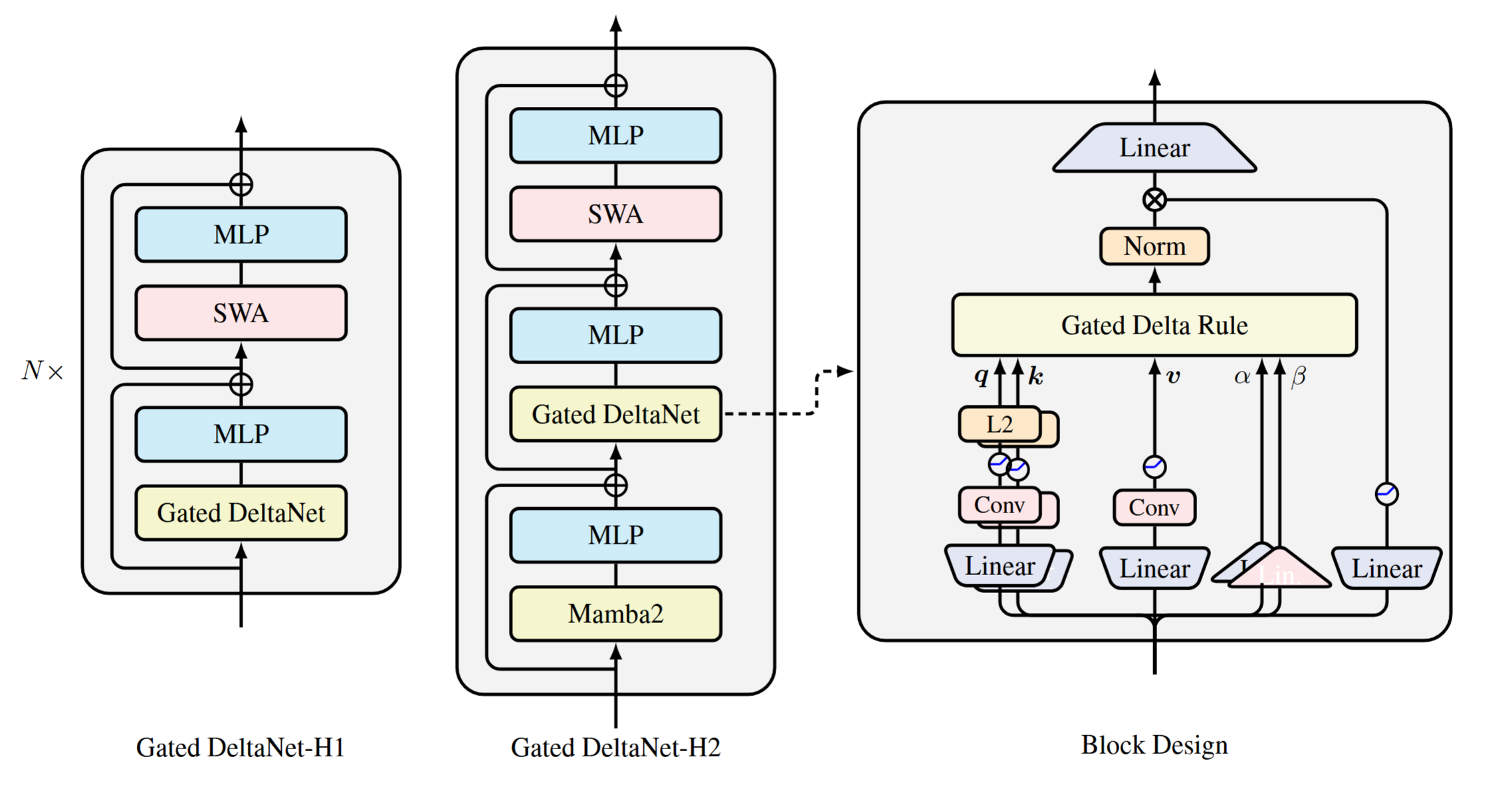
Gated DeltaNet¹⁰

• DeltaNet: precise modification of a single key-value pair. $${\mathbf{S}}_t={\mathbf{S}}_{t-1}-{\beta }_t\left({\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t\right){\mathbf{k}}_t^{\top }$$
• Adds forgetting gate ${\alpha }_t\in (0,1)$ from Mamba2 to allow rapid context cleanup. $$\begin{array}{rl}{\mathbf{S}}_t& ={\alpha }_t{\mathbf{S}}_{t-1}-{\alpha }_t\cdot {\beta }_t{\mathbf{S}}_{t-1}{\mathbf{k}}_t{\mathbf{k}}_t^{\top }+{\beta }_t{\mathbf{v}}_t{\mathbf{k}}_t^{\top }\\ & \\ & \approx {\gamma }_t{\mathbf{S}}_{t-1}-{\eta }_t\left({\mathbf{S}}_{t-1}{\mathbf{k}}_t-{\mathbf{v}}_t\right){\mathbf{k}}_t^{\top }\end{array}$$
• Given the update rule, the loss function can be derived as: $$\mathcal{L}=\frac{1}{2}{\Vert \mathbf{S}\mathbf{k}-\mathbf{v}\Vert }^2+\underset{\text{regularization}}{\underbrace{\frac{1-\gamma }{\eta }{\Vert \mathbf{S}\Vert }_F^2}}$$

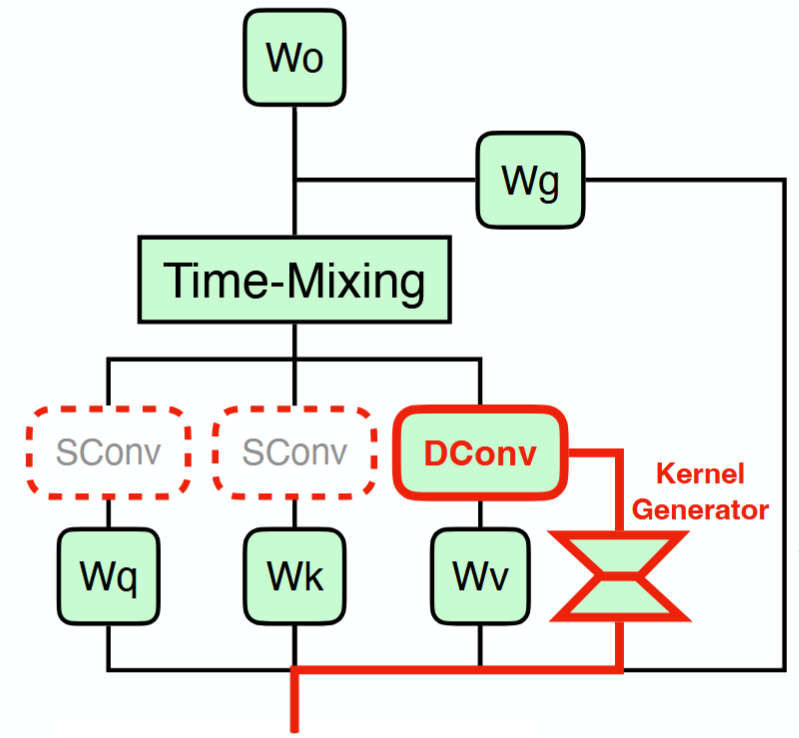
JetBlock & Jet Nemotron¹¹

Based on Gated DeltaNet:

• Remove convolution on query and key.
• Dynamic convolution on value.
  • Low-rank kernel generator with SiLU activation.

Linear Attentions in the Wild

Model	Attention	Hybrid	Size	Date
MiniMax-M1	Lightning Attention (GLA)	7:1	456B (A46B)	2025.06
Qwen3-Next-80B-A3B	GDN (& Gated Attention)	3:1	80B (A3B)	2025.09
IBM Granite-4.0	Mamba-2	9:1	3B~32B (A3B)	2025.10
Kimi Linear	Kimi Delta Attention (GDN + GLA)	3:1	48B (A3B)	2025.10
DeepSeek-V3.2-Exp	DeepSeek Sparse Attention	❌	671B (A37B)	2025.09

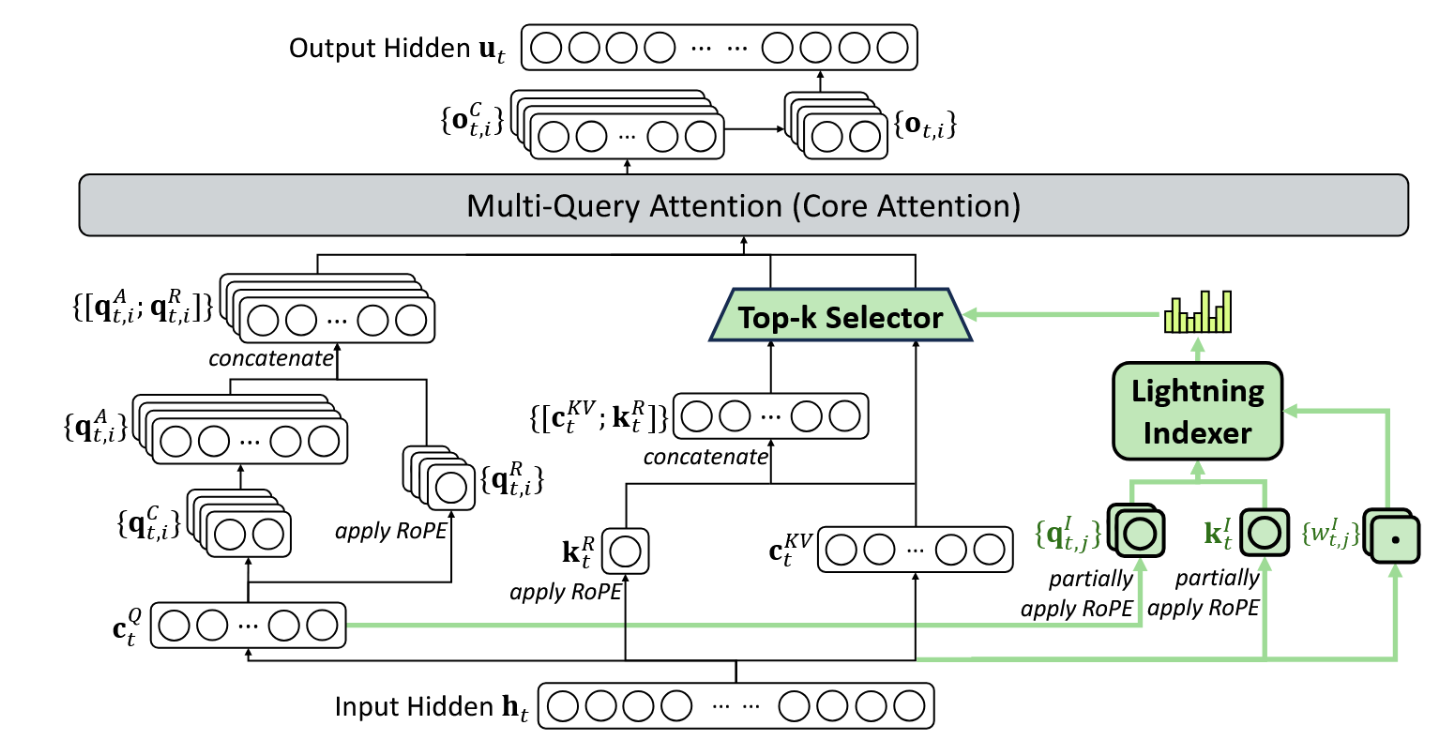
Notes on Deepseek Sparse Attention (DSA)¹²

• DSA is not linear attention.
• It is more like a full softmax attention with an additional top-k operator that selects only the token pairs worth attending to.
• The importance of a token pair is determined by a lightning indexer.
• Given that the index head dimension $H^I$ is small, the computation of the lightning indexer is small compared to the full attention. Nevertheless, the complexity of the attention part can be reduced from $O(n^2)$ to $O(nk)$, where $k$ is index_topk.
• Therefore, DSA can still be seen as subquadratic.

MiniMax-M1 vs. M2¹³

• MiniMax-M1 utilizes GLA, while MiniMax-M2 reverts to full softmax attention.
• Full Attention still holds practical advantages across various scenarios (code/math, agents, multimodal tasks, long chain-of-thought, RL, low-precision compute, speculative decoding, etc.).

Issues

• Evaluation Difficulty
  • Existing benchmarks are easy to maxed out.
  • High observation cost: scaling up, more complex evaluation.
• Infrastructure Gaps for Efficient Attention
  • Training: efficient attentions are often memory-bound without deep IO optimizations.
  • Inference:
    • Theoretical compute/memory savings only happens for long-enough sequences.
    • Challenges: low-precision state storage, efficient prefix caching, speculative decoding improvements.

Conclusion & Takeaways

• Linear attention is about striking the right balance between performance and efficiency.
  • Performance: gating, memory update.
  • Training Efficiency: stick to chunkwise parallel form.
  • Inference Efficiency: constant-size state/memory.
• Adoption is slowly increasing, but still far from mainstream.
  • Infrastructure is far behind softmax attention.

Footnotes

1. 苏剑林. (Jun. 20, 2025). 《线性注意力简史：从模仿、创新到反哺 》[Blog post]. Retrieved from https://kexue.fm/archives/11033 ↩

2. Sun, Yutao, et al. “Retentive network: A successor to transformer for large language models.” arXiv preprint arXiv:2307.08621 (2023). ↩ ↩² ↩³

3. Katharopoulos, Angelos, et al. “Transformers are rnns: Fast autoregressive transformers with linear attention.” International conference on machine learning. PMLR, 2020. ↩

4. Schlag, Imanol, Kazuki Irie, and Jürgen Schmidhuber. “Linear transformers are secretly fast weight programmers.” International conference on machine learning. PMLR, 2021. ↩

5. Mao, Huanru Henry. “Fine-tuning pre-trained transformers into decaying fast weights.” arXiv preprint arXiv:2210.04243 (2022). ↩

6. Gu, Albert, and Tri Dao. “Mamba: Linear-time sequence modeling with selective state spaces.” First conference on language modeling. 2024. ↩

7. Dao, Tri, and Albert Gu. “Transformers are ssms: Generalized models and efficient algorithms through structured state space duality.” arXiv preprint arXiv:2405.21060 (2024). ↩

8. Yang, Songlin, et al. “Gated linear attention transformers with hardware-efficient training.” arXiv preprint arXiv:2312.06635 (2023). ↩

9. Yang, Songlin, et al. “Parallelizing linear transformers with the delta rule over sequence length.” Advances in neural information processing systems 37 (2024): 115491-115522. ↩

10. Yang, Songlin, Jan Kautz, and Ali Hatamizadeh. “Gated delta networks: Improving mamba2 with delta rule.” arXiv preprint arXiv:2412.06464 (2024). ↩

11. Gu, Yuxian, et al. “Jet-Nemotron: Efficient Language Model with Post Neural Architecture Search.” arXiv preprint arXiv:2508.15884 (2025). ↩

12. DeepSeekAI. “DeepSeek-V3.2-Exp: Boosting Long-Context Efficiency with DeepSeek Sparse Attention.” GitHub (2025). ↩

13. See reddit post. ↩