SpinQuant

Summary

• A collection of applicable rotation parameterization.
• Learned rotation matrices.

Motivation

• Outliers are hard to quantize.
• Random rotation matrices and random Hadamard matrices exhibit non-negligible variance in accuracy.

Is it possible to optimize the rotation to maximize the benefit of quantization?

Methodology

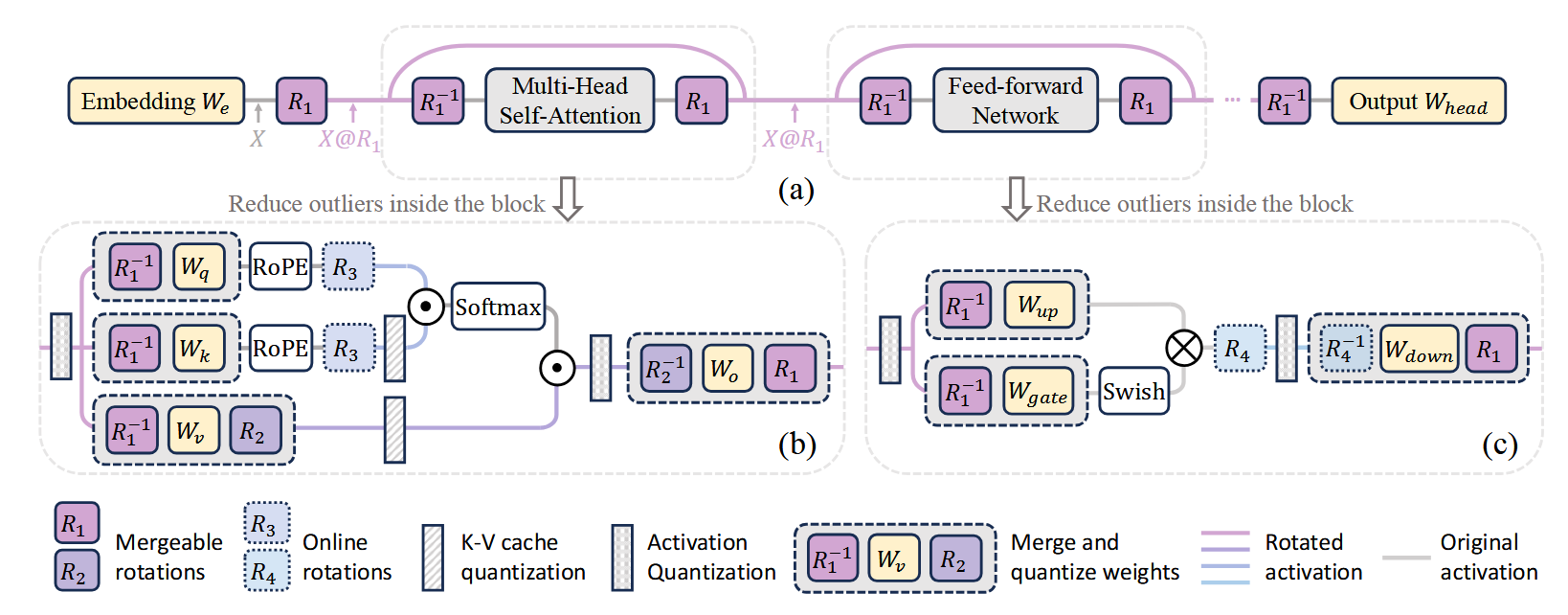
• Mergeable rotations ${\mathbf{R}}_1,{\mathbf{R}}_2$, i.e. residual and attention block, are learnable.
  • Use Cayley SGD on Stiefel manifold to learn ${\mathbf{R}}_1,{\mathbf{R}}_2$.
  • Loss: model loss, e.g. cross entropy.
  • It looks like the whole model shares the same ${\mathbf{R}}_1,{\mathbf{R}}_2$?
• Online rotations ${\mathbf{R}}_3,{\mathbf{R}}_4$ use random Hadamard transform.
• GPTQ can be incorporated by the following approach:
  1. Use SpinQuant to optimize network where only activation quantization is enabled.
  2. After the rotation matrices are determined, use GPTQ to quantize the weights.